Fig. 1
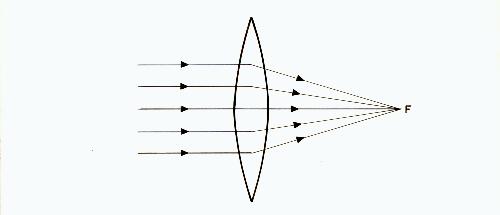
Fig. 2
Chapter 4
REFRACTIVE ERROR AND LENSES
Part 1: Spherical Lenses and Refractive Error
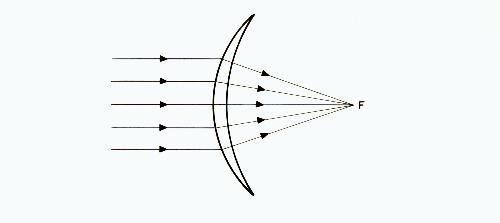
We have already covered what a concave or minus lens is. The other type of spherical lens is a convex or plus lens and it can be represented as in figures 1 and 2.

Fig. 1

Fig. 2
Note that both figures show a lens that is thicker at the center than at the periphery. Figure 1 is the usual form used in eyeglasses or contact lenses. Figure 2 is a simplified form that will be used in the diagrams that follow. The power of both plus and minus lenses is expressed in diopters.
A good way to remember the difference in appearance of a concave lens and a convex lens is to think of a concave lens as being the type that is hollowed out in the center, like a cave. Also, just as caves can be dangerous places, concave lenses can be dangerous to our vision.
The reason that these plus and minus lenses are called spherical is that their surfaces are uniformly curved, like the surface of a sphere or round ball.
The lens in figure 2 causes parallel rays to come to a focus at F, the focal point. The distance from the lens to point F is called the focal length of the lens and is an indication of how powerful the lens is.
If the distance from the lens to F is one meter, the lens is said to have a power of one diopter, usually abbreviated as 1 D. Since it is a plus lens, the complete description would be a +1 D lens.
If the distance from the lens to the focal point was one-half meter, this would he a +2 D lens and it would be twice as powerful as a +1 D lens. The following table shows this relationship more clearly:
| Focal Length in Meters | Lens Power in Diopters |
|---|---|
| 5 | 1/5 or 0.2 |
| 4 | 1/4 or 0.25 |
| 3 | 1/3 or 0.33 |
| 2 | 1/2 or 0.50 |
| 1 | 1 |
| 1/2 | 2 |
| 1/3 | 3 |
| 1/4 | 4 |
| 1/5 | 5 |
Note that the numbers in one column are the reciprocals of the numbers in the other column. The reciprocal of a fraction is obtained by turning it upside down. Thus the reciprocal of 1/2 is 2/1 or 2. Working in the opposite direction, 2 can be expressed as 2/1 and its reciprocal is 1/2. The power of concave lenses is expressed in a similar way, that is, -1, -2, -3, etc., even though such lenses do not have a real focal point. They have an imaginary focal point, and it is for this reason that they are called minus lenses and convex lenses are called plus lenses.
Diopters can be added together or subtracted from each other. In other words, three +1 D lenses are equal optically to one +3 D lens. A -4 D lens together with a +1 D lens is equivalent to a -3 D lens. Note in the table that as the lens powers increase, the change in focal length is less. For example, the distance from 1/4 to 1/5 meter is much less than the distance from 1 to 1/2 meter.
The lenses used by the optical industry are usually made available in 0.25 D steps such as 1 D, 1.25 D, 1.5 D, 1.75 D, etc. Steps smaller than 0.25 D are seldom needed. Zero power lenses are called plano - that is, they are similar to window glass.
Diopters are also used in another way - to express the amount of nearsightedness (or farsightedness) a person has. The nearsighted person who needs a -1 D lens to regain normal vision is said to have one diopter of myopia. By normal vision in this case we mean neither farsighted nor nearsighted. This was defined in an earlier chapter as emmetropia. The patient who needs a -2 D lens is said to have two diopters of myopia, and so forth.
Another way of expressing this is to say that the person has a refractive error of -1 D or -2 D. A farsighted person would be said to have a refractive error of +1 D, +2 D, etc. The word error means only that the refraction differs from emmetropia. It does not necessarily mean abnormal vision. For example, a small amount of farsightedness and a small amount of astigmatism (to be explained later) can be considered normal.
Diopters are also used on the eyeglass prescription. The prescription for the first pair of glasses for a nearsighted person might call for -1 D lenses. If we know that this prescription has been written to bring the vision hack to normal and not for some other reason, it tells us that the person's far point, or limit of clear vision, is one meter from the eyes. Everything beyond that is blurred. This is a typical prescription for a beginning myope since a refractive error of -1 D is enough to make distant objects, such as a blackboard, rather blurred. If the prescription were for -2 D lenses, we would know that the limit of clear vision is only 1/2 meter from the eyes. A prescription of -3 D means the far point is only 1/3 meter from the eyes.
This idea can be continued by referring again to the above table. Keep in mind though, since the information will be useful later, that 1/3 meter (33 1/3 centimeters) is the approximate distance at which most people hold a book. Expressed in another way, a -3 D myope (a person who needs -3 D lens for clear distance vision) who reads without glasses with the book held at 1/3 meter is reading without having to accommodate at all. The eyes are focused for distance. In theory, if the person never wore glasses, the myopia progression would stop at this amount since no accommodation is used. It is normally only the use of minus glasses that causes the myopia to increase beyond this amount.
If a child is fitted with, for example, -0.5 D lenses at age six, typical myopia progression might require -1 D lenses at age seven, -1.50 D at age eight, etc. When talking about the average amount of progression in myopic children, the figure most often used is 0.5 D per year. Naturally, the younger a child is when myopia starts the more years will be available for the myopia to increase, until the child becomes an adult and the eyes become less adaptable.
In persons with very high myopia, the necessary corrective lenses can be over -20 D in power. Myopia could be classified according to degree as follows:
| Diopters | Degree |
|---|---|
| 0 to 3 | low |
| 3 to 6 | moderate |
| over 6 | high |
Each 3 D of myopia corresponds to an increase in the length of the eye of 1 mm. Therefore, a 21 D myope would have eyes which are 7 mm longer than would be normal for that person. It is not surprising that these high myopes run the risk of detached retina.
Part 2: Cylindrical Lenses and Astigmatism
Although most people are familiar with the word astigmatism, few really know what it means. It frequently accompanies myopia and for this reason deserves some discussion here.
In the diagrams in previous chapters, it was assumed that the lens of the eye was symmetrical or uniform in shape. For example, light rays passing through the top of the lens would be bent just as much as rays passing through the bottom or sides of the lens. Such a lens would have a surface something like the surface of a round ball - the curvature being the same in all directions. Now suppose that you were holding a flexible ball between your hands. If you were to deform the ball by compressing the sides with your hands, the surface of the ball facing you would no longer be uniform. It would curve more in a horizontal direction than in a vertical direction. (This shape can also he visualized by thinking of the surface of an automobile tire.) Either the lens or cornea of the eye (or both) can take a similar shape, causing the refractive error called astigmatism. Although most astigmatism is due to corneal irregularities, we will continue to use the lens in our examples for the sake of simplicity.
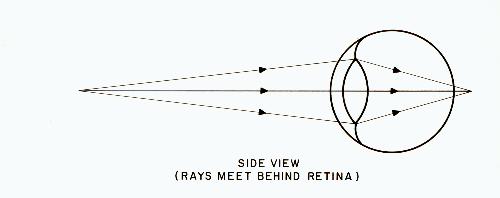
Fig. 3
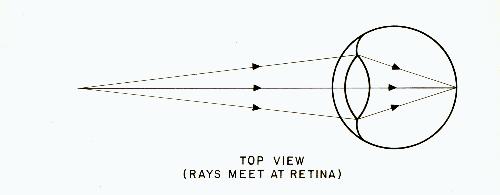
Fig. 4
Figures 3 and 4 show an eye where the horizontal lens curvature is greater than the vertical. Figure 3, which is a side view, shows the rays passing through the top and bottom of the lens. Figure 4, which is a top view, shows the rays passing through the sides of the lens. In this simplified case, the cornea is assumed to be free of astigmatism.
It can be seen that while the rays passing through the sides of the lens come to a focus on the retina (as in the top view), the rays passing through the top and bottom of the lens do not (as in the side view). If this eye was to accommodate so that the top and bottom rays come to a focus on the retina, then the rays coming through the sides of the lens would fall short of the retina. In other words, there is no way for the eye to focus all the rays on the retina at the same time.
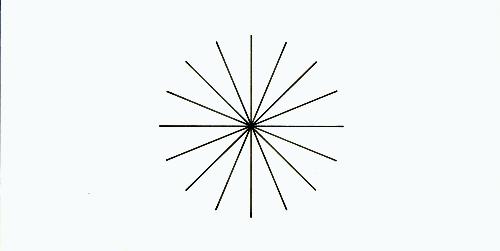
Fig. 5
The practical significance of this refractive error can be understood by looking at figure 5 with one eye at a time. If some spokes of the wheel seem clearer than others (that is, if they are darker), then you have some astigmatism.
Usually the astigmatism is not great enough to cause poor vision or to require the use of corrective lenses. When astigmatism is corrected, it is done with the use of cylindrical lenses, whereas the concave and convex lenses described in preceding chapters are spherical lenses.
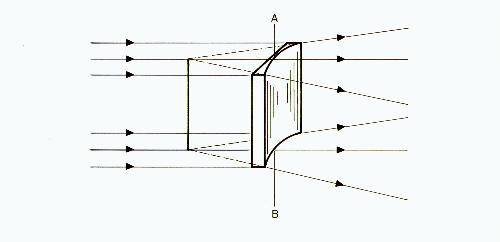
Fig. 6
A concave cylindrical lens is shown in figure 6, and a convex cylindrical lens in figure 7.
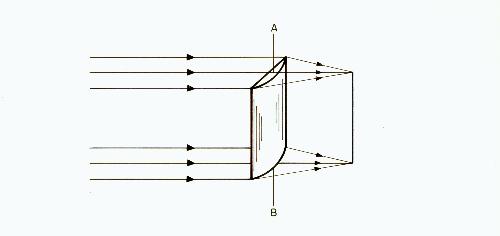
Fig. 7
Line AB indicates the axis of the lens. Note that rays passing through the axis are not bent.
When both a cylindrical and spherical correction are needed, they are ground on the same lens.
The location of the axis of a cylindrical lens must he specified when it is placed before the eye. Figure 8 shows the usual method of designating the angle of the axis.
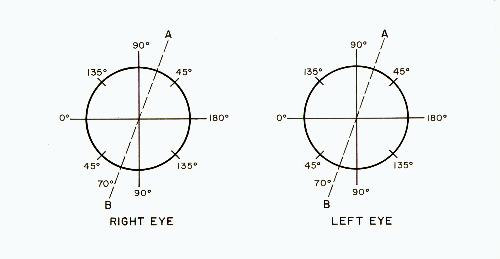
Fig. 8
A similar notation is used for each eye. The observer is facing the eyeglass wearer and the zero is at the observer's left. The scale is read below the horizontal line with 90o at the bottom and 180o at the right.
As an example, if a cylindrical lens was placed with its axis along line AB, it would be at an angle of 70o.
A refractive error can take one of the following forms:
In an earlier chapter it was pointed out that if myopia is fully corrected with minus lenses, this tends to "lock" the defect on the eye so that the vision can only get worse, not better. A somewhat similar situation can exist with astigmatism. If astigmatism is fully corrected with a cylindrical lens, it may tend to lock the astigmatic defect on the eye and prevent its improvement. As a general rule, all corrective lenses tend to preserve the defect they are "correcting."
Astigmatism, like myopia, can vary somewhat from one examination to the next. Furthermore, it is possible for astigmatism to increase as a result of a ciliary spasm, and it can improve as the ciliary spasm relaxes. It is a sort of "secondary effect" of the main problem in such cases. It is probably for this reason that astigmatism is especially associated with myopia. Myopic astigmatism is the most common form of astigmatism, and the greater the spherical error the greater the tendency to a greater astigmatic error. Fully correcting such astigmatism could hinder the relaxation of the spasm and the corresponding decrease in the myopia.
Therefore, if the astigmatism is not bad enough to cause problems, it should not be corrected. If the astigmatism is bad enough to require some correction, every consideration should be given to prescribing an undercorrection.
Often, when astigmatism occurs inside the eye as well as at the cornea, the astigmatism inside the eye is just opposite in amount to the corneal astigmatism. The two forms of astigmatism thus cancel each other and leave the eye with no significant amount of astigmatism. Researchers believe that it is the normal pressure of the eyelids on the top and bottom of the cornea that causes this corneal astigmatism in many people. Nature, in its wisdom, then compensates for this by creating the opposite amount of astigmatism inside the eye, primarily in the lens.
Since nearly everyone has some astigmatism, it is easy for an unscrupulous eye doctor to say, "I'm going to prescribe glasses for you since you have astigmatism", even if the astigmatism causes no problems. Astigmatism may sound like something terrible but in most people, it is unimportant and can be ignored.
Part 3: Prismatic Lenses
Prismatic lenses are used in eyeglasses, not to change the focus of light rays, but to change their direction.
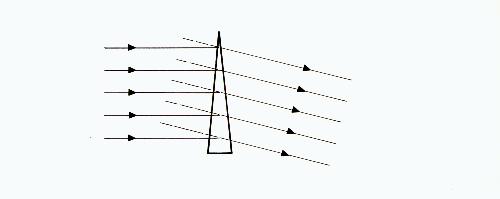
Fig. 9
Figure 9 shows a simplified form of a prismatic lens. Note that the parallel rays entering the left side of this lens are still essentially parallel when leaving the right side. If the eye is located on the right side of the lens, the dotted lines show where the eye believes the rays are coming from. The viewed object thus appears to be higher than it actually is. As you will note from figure 9, light rays are always bent toward the base or thick portion of the prism. The viewed object thus appears to be displaced toward the apex or top of the prism.
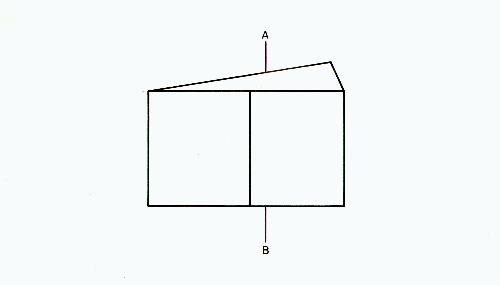
Fig.10
Figure 10 shows how vertical line AB, viewed through a prism, appears to be displaced toward the apex of the prism. Keep in mind that the accommodation of the eyes is not affected by prisms. Only the direction from which the light rays come is changed. Some types of prisms are capable of separating light into its various colors, but the thin prisms used in eyeglasses do not do this. Prisms are frequently used to solve problems with the external muscles of the eyes. For example, a person who has difficulty converging (turning the eyes toward the nose) for close work could be given base-in prisms (with the base toward the nose) before each eye, reducing the amount of convergence necessary.
Part 4: How To Read Your Prescription
The relationship between refractive error and visual acuity needs to be explained at this point. Many people are familiar with the method of expressing distance visual acuity by figures like 20/20, 20/30, 20/100, etc. The expression 20/100, for example, means that the person can read letters on a wall chart at twenty feet that a person with normal vision can read at one hundred feet. In the metric system the unit of length is the meter and figures such as 6/6, 6/9, and 6/12 are used.
The following chart makes clearer the relationship between these quantities:
| Visual Acuity in Feet | Visual Acuity in Meters | Refractive Error in Diopters |
|---|---|---|
| 20/20 | 6/6 | 0 |
| 20/30 | 6/9 | -0.50 |
| 20/40 | 6/12 | -0.75 |
| 20/50 | 6/15 | -1.00 |
| 20/70 | 6/20 | -1.25 |
| 20/100 | 6/30 | -1.50 |
| 20/150 | 6/45 | -2.00 |
| 20/200 | 6/60 | -2.50 |
| 20/250 | 6/75 | -3.00 |
The right-hand column gives the approximate prescription that would be needed to see normally. This is to say that there is not a rigidly fixed relationship between refractive error and visual acuity. Two people who have the same refractive error and need the same prescription may have widely different degrees of success in reading a distant wall chart with their glasses removed. This chart is based on the average of many people and cannot be used for accurately predicting either the visual acuity or the refractive error of any particular individual. It is included here merely for information purposes.
A vision specialist could do a fairly good job of determining your refractive error just by using a wall chart. This is done by putting various combinations of lenses in the trial frame and asking you how well you can see, until the best combination of powers has been determined. This method is called a subjective method since the person must cooperate and be able to give correct answers. Usually, more sophisticated examination methods are also used, in which the examiner looks into the eye with a special instrument and determines the refractive status.
Many people have refractive errors of -3 D and above. It only requires a few changes of glasses to reach this point. Note from the chart that -3 D myopes frequently have a visual acuity of about 20/250. In the United States, a person with a visual acuity of 20/200 or worse is considered legally blind. Naturally, this definition only applies to those people whose vision cannot be corrected to better than 20/200 with glasses. Such people usually have vision problems which give them poor vision for close work also. A -3 D myope who can attain 20/20 vision with glasses is much more fortunate.
The point to be stressed here is that if your child is fitted with a pair of minus lenses, and if this first prescription is followed by yet stronger prescriptions, you will soon have a child who is legally blind without the crutch of glasses. Sadly, many children attain vision that is this poor even before they pass the age of ten.
Prescriptions for contact lenses are more complicated than for eyeglasses and will not be discussed here.
A typical prescription for a myope might look something like this:
The term "O.D." stands for oculus dexter and means right eye. The term "O.S." stands for oculus sinister and means left eye. Do not confuse this O.D. with the O.D. found after an optometrist's name, where it means Doctor of Optometry.
Since both of the eyes are the same in the above prescription, it can also be written -1.00 O.U. The term O.U. stands for oculus uterque and means that the -1.00 applies to both eyes.
Some prescriptions are written with R.E. for right eye and L.E. for left eye, and we will use this terminology in the descriptions that follow. Sometimes the specialist will eliminate the decimal points and write 100 for 1.00 and 50 for 0.50.
Here is another, more complicated prescription:
The right eye requires only a -3.50 spherical lens. However, the left eye requires a -2.50 spherical lens coupled with a -1.00 cylindrical lens with its axis at an angle (denoted by the symbol "x") of 90o. Both corrections are ground on the same lens. This astigmatic correction at 90o tells us that the sides of the lens of the eye are more myopic than the top and bottom so that more power is needed at the sides. By adding -2.50 and -1.00 together we get -3.50, indicating that the sides of the lens of the left eye are just as myopic as the entire lens of the right eye. If necessary, a prismatic correction can also be added to the prescription.
You should now be able to read a simple eyeglass prescription and better understand what is happening to your eyes or your child's eyes.
If you already have a pair of glasses and you want to know what the prescription is for them, you don't have to return to the doctor who prescribed them. Take them to any optician's shop and the prescription can be determined by testing them on a special machine.
There is also a simple test that you can do yourself to determine whether your glasses are of the plus or minus type. Remove your glasses and hold them a short distance in front of you. Look through one of the lenses at an object across the room. Then move your glasses up and down or sideways. If the viewed object moves in the same direction as the lens, the lens is minus. If the viewed object moves in the opposite direction, the lens is plus. If the direction of movement is not readily apparent it is possible that the difficulty is due to an astigmatic correction in the lens.